3-body simulation with python

While watching the 3 Body Problem series on Netflix I wasn't marveling at the plot twists or ideas presented. Partly because I've read the source, but mostly because I've taken up so much science fiction in my life that finding something truly new is rare for me.

Still, it had me thinking that I've never really coded anything based in real physics. Apart from couple of demos in Unity, I've been comfortable in the abstract domain.

So I've decided to rectify that error, coding a simple simulation of the aforementioned problem.

I've decided to do the work in Python, which meant that it won't exactly break any performance records, but that wasn't really the point. After all, there are far better simulations available of n-particle/body systems than I could ever make.

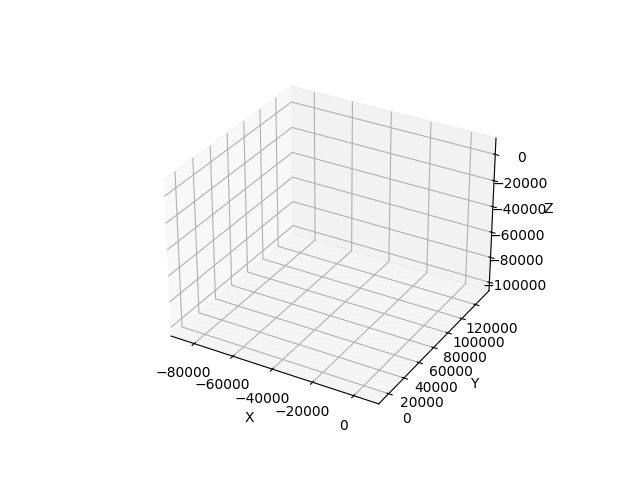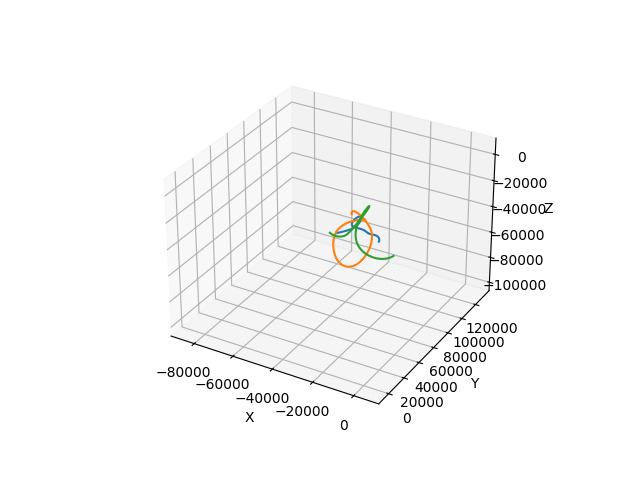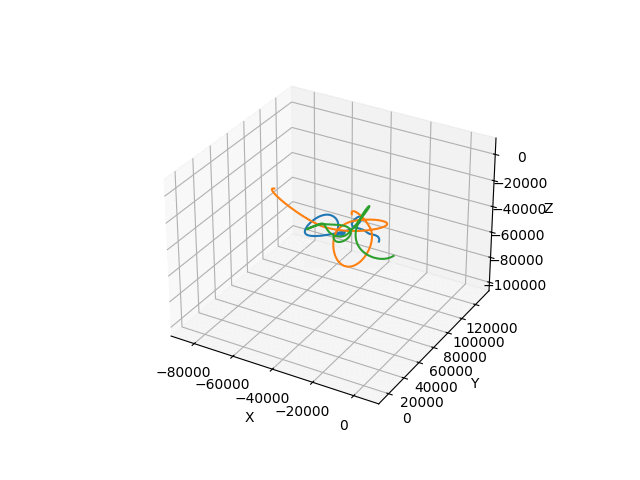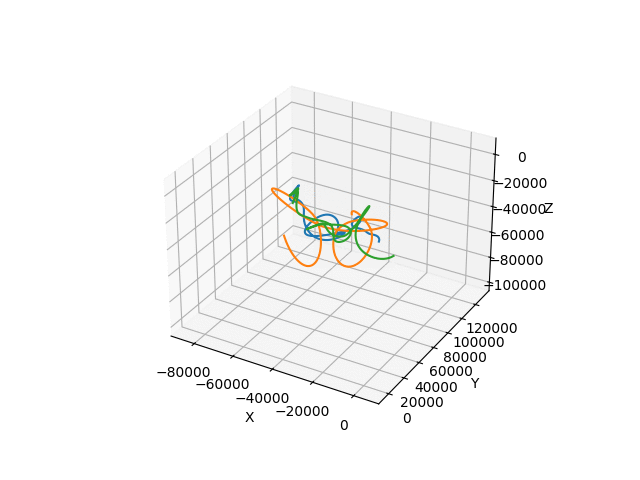
But to make things at least a bit manageable, I've chosen numpy to handle numerical side of things. Simulation itself consists of primary loop, computing mutual attraction vectors of all bodies in the system, their movement and updating their positions in the step.

The obvious way to simplify things would be to store all positions and vectors in matrices. But I didn't really feel like it so I stuck with OOP approach, making each body it's own object.

This does have some overhead, but it's somewhat easier to follow.

The bigger issue was presentation. Sure, printing coordinates and vectors to terminal is nice, but I want something nicer. My first attempt with matplotlib was looking relatively well. But it was a gif, and I felt that it wasn't nearly flexible enough. I had to record the history of object positions ahead of rendering them. Surely there was a better way.

I've decided to bite the bullet and venture into mystic realm of 3D rendering. The Panda3D seemed like a good choice. Open source, with bindings for Python and relatively simple API. I rewrote the main loop to work as a task method.

I've set the camera to always follow the common center of mass, and to be relatively far away, so all bodies would render together.
There was just one more thing to do. I made simple sphere model for bodies in the simulation, so I wouldn't have to watch bunch of pandas floating around. Trust me it does make sense in the context.

Not exactly Crysis level technology, but I think it was a nice exercise. Maybe at some point I'll revisit it, rewriting the entire thing in C++ for example.